Check the validity of each equation using the properties of the real numbers to see if they are true or false.
A
Starting with the expression:
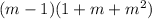
Use the distributive property to expand the second factor:
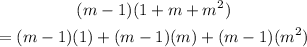
Use the same property to expand the factor (m-1) in each term. Simplify the expression:
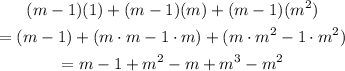
Notice that the term m cancels out with the term -m, and the term m^2 cancels out with the term -m^2. Therefore:
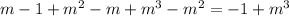
Therefore:
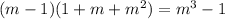
Therefore, the equation A is true.
B
Expand the term (n+3)^2 and add 2n to see if it is equal to 8n+13.
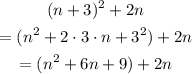
Add the like terms 6n and 2n:

Which cannot be equal to 8n+13 since there is a quadratic term.
Therefore, the equation B is false.