Question

The inclination (tilt) of an amusement park ride is accelerating at a rate of 2160 degrees/min^2. What is the ride's acceleration in degrees/s^2?

Answer 1

`\bf \begin{array}{llll} minutes&seconds\\ ------&------\\ 1m&60s\\\\ (1m)^2&(60s)^2\\ m^2&3600s^2\\\\ (1m)^3&(60s)^3\\ m^3&216000s^3 \end{array}\\\\ -------------------------------\\\\ \cfrac{2160^o}{\underline{m^2}}\cdot \cfrac{\underline{m^2}}{3600~s^2}\implies \cfrac{2160^o}{3600~s^2}\implies \cfrac{3^o}{5~s^2}\implies 0.6(deg)/(s^2)`

Answer 2

Solution: The acceleration of ride in degrees per second square is 0.6 degree/
`s^2`.

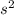Step-by-step explanation:

It is given that the inclination of the amusement park ride is accelerating at a rate of 2160 degree/
`s^2`.

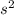Since we know that 1 minute = 60 seconds.

`1 min^2=3600sec^2`

`3600^(\circ)/min^2=1^(\circ)/sec^2`

`1^(\circ)/min^2=(1)/(3600)^(\circ)/sec^2`

`2160^(\circ)/min^2=(2160)/(3600)^(\circ)/sec^2\\`

`2160^(\circ)/min^2=0.6^(\circ)/sec^2`

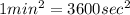
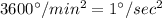
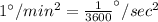
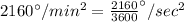
Therefore, the The acceleration of ride in degrees per second square is 0.6 degree/
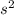`s^2`.