Let V be the number of containers of vanilla ice cream that Manny uses, and P be the number of peach ice cream containers that Manny needs to obtain 11 containers at a cost of $8 each. Then we can set the following system of equations:
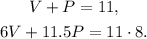
Solving the first equation for V we get:
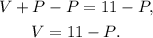
Substituting the above equation in the first one we get:
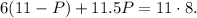
Simplifying the above equation we get:

Subtracting 66 from the above equation we get:
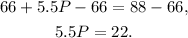
Dividing the above equation by 5.5 we get:
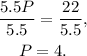
Finally, substituting P=4 in V=11-P we get:
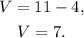
Answer: Manny needs 7 containers of vanilla ice cream and 4 containers of peach ice cream.