Question

The sample mean is x = 12.8%. let x be a random variable that represents the percentage of wheat crop in that county lost to hail. assume that x has a normal distribution and σ = 5.0%. do these data indicate that the percentage of wheat crop lost to hail in that county is different (either way) from the national mean of 11%? use α = 0.01.

Answer 1

Given that
`\bar{x}=12.8\%` and
`\sigma=5.0\%`, given that the population mean is
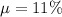
`\mu=11\%` and the sample size is n = 16, the test statistic is given by


`z= \frac{\bar{x}-\mu}{\sigma/√(n)} \\ \\ = (12.8-11)/(5/√(16)) \\ \\ = (1.8)/(5/4) = (1.8)/(1.25) \\ \\ =1.44 \\ \\ \Rightarrow p-value=p(z\ \textgreater \ 1.44) \\ \\ =1-P(z\ \textless \ 1.44)=1-0.92507 \\ \\ =0.07493`

Since the test is a two tailed test, the p-value is 2(0.07493) = 0.14986

Since the p-value is greater the significant level of α = 0.01, thus, we fail to reject the null hypothesis and conclude that there is no sufficient evidence that the percentage of wheat crop lost to hail in that county is different from the national mean of 11%.