Question

The length of a rectangle is increasing at a rate of 8 cm/s and its width is increasing at a rate of 6 cm/s. when the length is 13 cm and the width is 5 cm, how fast is the area of the rectangle increasing?

Answer 1

Given :

The length of a rectangle is increasing at a rate of 8 cm/s and its width is increasing at a rate of 6 cm/s.

When the length is 13 cm and the width is 5 cm .

To find :-

how fast is the area of the rectangle increasing?

Solution :-

As we know that :-

A = lb

To find the rate :-

d(A)/dt = d(lb)/dt .

Differenciate :-

dA/dt = l (db/dt ) + b (dl/dt )

Substitute :-

dA/dt = 13*7 + 5* 8

dA/dt = 91 + 40 cm²/s

dA/dt = 131 cm²/s

Answer 2

L(t) = 13 + 8t ............(1)
W(t) = 5 + 6t .............(2)
Let the area be A.
A(t) = (13 + 8t)(5 + 6t) ...(3)
Expanding the brackets in (3), we get:

`A(t)=48t^(2)+118t+65\ ..........(4)`
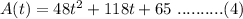
Differentiating A with respect to time gives:

`(dA)/(dt)=96t+118`
When t = 0, the rate of change of the area of the rectangle is:
`(dA)/(dt)=118`
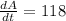
Therefore the answer is 118 square cm per second.