Question

Find the equation of the line that is parallel to the line in Problem 2 and passes through the point (-2,-4).Problem 2 is: Graph the equation 3x + 5y = 30

Answer 1

GIVEN:

We are given the equation of the line as shown below;

`3x+5y=30`

Required;

To find the equation of the line that is parallel to the one given and that passes through the point,

`(-2,-4)`

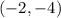
Step-by-step solution;

To solve this math problem, we begin by re-writing the given equation in slope-intercept form, which is;

`y=mx+b`

Note that in this equation, the letter m represents the slope of the line.

`\begin{gathered} 3x+5y=30 \\ \\ Subtract\text{ }3x\text{ }from\text{ }both\text{ }sides; \\ \\ 3x-3x+5y=30-3x \\ \\ 5y=30-3x \\ \\ Divide\text{ }all\text{ }terms\text{ }by\text{ }5; \\ \\ (5y)/(5)=(30)/(5)-(3x)/(5) \\ \\ y=6-(3)/(5)x \end{gathered}`

Next step, we re-arrange the terms as shown in the equation above;

`\begin{gathered} y=6-(3)/(5)x, \\ \\ Becomes; \\ y=-(3)/(5)x+6 \end{gathered}`

The coefficient of x (that is the variable m) is -3/5. We now have the slope.

Next, take note that where you are given two parallel lines, their slopes are equal. That means for the equation we are yet to determine the slope is also -3/5.

For the parallel line, we have;

`\begin{gathered} m=-(3)/(5) \\ \\ (x,y)=(-2,-4) \end{gathered}`

Now we can substitute these into the equation in slope-intercept form and we have;

`\begin{gathered} y=mx+b \\ \\ -4=-(3)/(5)(-2)+b \\ \\ -4=-(6)/(5)+b \\ \\ Add\text{ }(6)/(5)\text{ }to\text{ }both\text{ }sides; \\ \\ (6)/(5)-4=(6)/(5)-(6)/(5)+b \\ \\ (6-20)/(5)=b \\ \\ -(14)/(5)=b \end{gathered}`

Now we have the values of m (the slope) and b (the y-intercept) and we can now apply this to write out the equation for a line parallel to the one given;

`\begin{gathered} y=mx+b, \\ \\ Where\text{ }m=-(3)/(5),\text{ }b=-(14)/(5) \\ \\ y=-(3)/(5)x+(-(14)/(5)) \\ \\ y=-(3)/(5)x-(14)/(5) \end{gathered}`

The equation therefore is;

ANSWER:

`y=-(3)/(5)x-(14)/(5)`