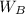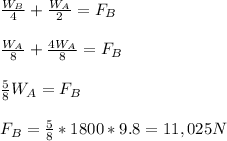Question

A uniform steel beam has a mass of 1800 kg. on it is resting half of an identical beam, as shown in fig. 9-44. what is the vertical support force at each end? left end n (upward) right end n (upward)

Answer 1

Support force at side A: 15,435 N

Support force at side B: 11,025 N

Step-by-step explanation:

Part A:

Because we are looking for the force at side A, we set
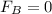`F_B=0` for easier calculations.

Recall that:

`\sum\tau=0; \tau=F_\perp*r; W=m*g`

And given that:

`W_B=(1)/(2)W_A`

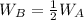
Where
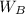`W_B` is the weight of the smaller mass.

Hence:

`(-W_B*(3L)/(4))-(W_A*(L)/(2))+(F_A*L)=0\\\\((W_B*(3L)/(4)) + (W_A*(L)/(2)))/(L)=F_A`

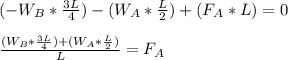
Substitute
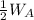`(1)/(2)W_A` for
`W_B`

`(3W_B)/(4)+(W_A)/(2)=F_A\\\\(3W_A)/(8)+(4W_A)/(8)=F_A\\\\(7)/(8)W_A=F_A\\\\F_A=(7)/(8)*1800*9.8=15,435 N`

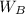
Part B:

Because we are looking for the force at side B, we set
`F_A=0` for easier calculations.

Recall that:

`\sum\tau=0; \tau=F_\perp*r; W=m*g`

And given that:

`W_B=(1)/(2)W_A`

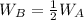
Where
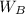`W_B` is the weight of the smaller mass.

Hence:

`(-W_B*(L)/(4))-(W_A*(L)/(2))+(F_B*L)=0\\\\((W_B*(L)/(4)) + (W_A*(L)/(2)))/(L)=F_B`

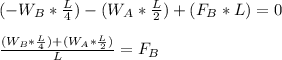
Substitute
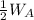`(1)/(2)W_A` for
`W_B`

`(W_B)/(4)+(W_A)/(2)=F_B\\\\(W_A)/(8)+(4W_A)/(8)=F_B\\\\(5)/(8)W_A=F_B\\\\F_B=(5)/(8)*1800*9.8=11,025 N`

Answer 2

Let the left end A and the right end B.
Let w = the weight of the full beam.
0 = -(w/2)*(L/4) - (w)*(L/2) + Fa*L
Fa = [(w/2)*(L/4) + (w)*(L/2)]/L = w/8 + w/2 = 5/8*w = 5/8*m*g = 5/8*1800*9.81 Fa = 11036.25 N
Fa + Fb = w Fb = w - Fa = 1.8*(1800*9.81) - 11036.25 Fb = 20748.15 N