Question

Y - 4x^(3/2) from x=0 to x=1 The length of the curve is?

Answer 1

The length of a curve or arc length is equal to this definite integral:


`arc length= \int\limits^a_b {} \, ds`

Where


`ds= { \sqrt{1+ ( (dy)/(dx) )^(2) } }dx`

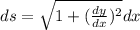
The curve seems to be
`y= 4x^(3/2)`

These are the calculations step by step:

1) dy/dx = 4*(3/2)x^(1/2) = 6x^(1/2)

2) length = ds = √ (1+ [6x^(1/2)]^2 ) dx = √ (1 + 36x)dx

3) ∫ds from a to b = ∫ √(1 + 36x) dx from a to b =

= (1/54) (1 + 36x)^(3/2) from a to b

a 0 and b = 1 => lentgh = (1/54) (1 + 36)^(3/2) - (1/54) (1)

=> length = 4.15

Answer: 4.15