Question

Among all pairs of numbers (x,y)such that 6x+2y=36 find the pair for which the sum of squares, x^2+y^2 is minimum.

Answer 1

First, we simplify 6x+2y=36 into 3x+y=18 by dividing by 2. This means that y=-3x+18.


The sum
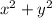
`x^2+y^2` can be written as:
`x^2+y^2=(x+y)^2-2xy`,

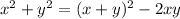
from the binomial expansion formula:
`(x+y)^2=x^2+2xy+y^2`.

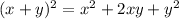Thus, substituting y=-3x+18 and simplifying we have


`x^2+y^2=(x+(-3x+18))^2-2x(-3x+18)`
`=(-2x+18)^2+6x^2-36x=4x^2-72x+18^2+6x^2-36x`
`=10x^2-108x+18^2`.

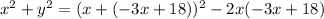
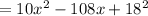This is a parabola which opens upwards (the coefficient of x^2 is positive), so its minimum is at the vertex. To find x, we apply the formula -b/2a. Substituting b=-108, a=10, we find that x is 108/20=5.4.


At x=5.4, the expression
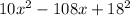`10x^2-108x+18^2`, which is equivalent to
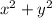`x^2+y^2`, takes it smallest value.

Substituting, we would find
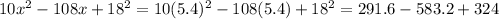`10x^2-108x+18^2=10(5.4)^2-108(5.4)+18^2=291.6-583.2+324`=32.4 This is the smallest value of the expression.


For x=5.4, y=-3x+18=-3(5.4)+18=1.8.



Answer: (5.4, 1.8)