Answer:
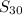 = 1455.
= 1455.
Explanation:
Given : an=3n+2.
To find : find the sum of the first 30 terms of the sequence.
Solution : We have given
 = 3n + 2.
= 3n + 2.
For first term n = 1
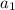 = 3 (1) +2.
= 3 (1) +2.
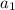 = 5
= 5
For last term n = 30
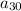 = 3(30) +2
= 3(30) +2
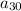 = 90 +2
= 90 +2
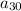 = 92.
= 92.
Then sum of first 30 terms
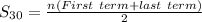 .
.
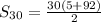 .
.
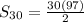 .
.
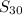 = 15 *97.
= 15 *97.
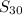 = 1455.
= 1455.
Therefore,
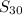 = 1455.
= 1455.