Question

An angle bisector of a triangle divides the opposite side of the triangle into segments 6 cm and 4 cm long. A second side of the triangle is 7.4 cm long. Find the longest and shortest possible lengths of the third side of the triangle. Round answers to the nearest tenth of a centimeter.

Answer 1

Let the third side be x. According to the angle bisector theorem, the following ratios can be written:

i) If 7.4 is larger than x, since 6>4 we have:


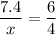
`\displaystyle{ (7.4)/(x)= (6)/(4)`. this yields x=(7.4*4)/6=4.93


ii) If x is larger than 7.4, since 6>4 we have:


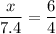
`\displaystyle{ (x)/(7.4)= (6)/(4)`. this yields x=(7.4*6)/4=11.1


Thus, the lengths are 11.1 cm and 4.9 cm