To find the volume of the space inside the cylinder that is not filled by the cone, we proceed as follows:
Step 1: Establish the relationship which will enable you obtain the volume, as below:
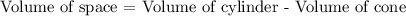
Step 2: Calculate the volume of the cylinder
The volume of a cylinder is given by the formula as below:

Now,
radius of the cylinder = (diameter)/2 = AC/2 = 16/2 = 8m
height of cylinder: ?
The height of the cylinder is gotten as follows:
We now apply the Pythagorean theorem to obtain the value of h, as follows:
![\begin{gathered} \text{hypothenus}^2=opposite^2+adjacent^2 \\ 17^2=h^2+8^2 \\ 289=h^2+64 \\ 289-64=h^2 \\ 225=h^2 \\ h^2=225 \\ h=\sqrt[]{225} \\ h=15m \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ejgta098cizs0m7x9gi3.png)
Therefore, the height of the cylinder is 15m
Therefore:
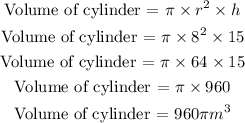
Step 3: Calculate the volume of the cone
The volume of a cone is given by the formula as below:

Now,
radius of the cone = (diameter)/2 = AC/2 = 16/2 = 8m
height of cone: 15m
Therefore:
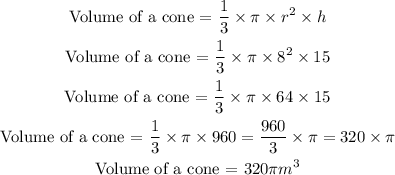
Finally, the volume of the space inside the cylinder that is not filled by the cone is:
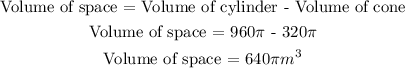
Correct answer: Option D