Answer:
If the optimum output is 500 units, the current profit is $ 15,940
Explanation:
As per the statement:
The profit function for the unit at the optimum output, x, is given by:

If the function f(x) models the current capacity of the unit.
⇒we substitute f(x) =0.80x for every x in the equation.
then;
the composite function giving the unit's current profit function is:
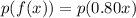
⇒
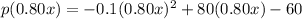
Simplify:-
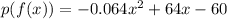 ....[1]
....[1]
We have to find the current profit.
If the optimum output is 500 units
⇒x = 500 units
Substitute in [1] we have;
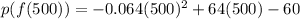
⇒
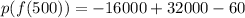
Simplify:
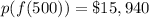
Therefore, the current profit is $15,940