Given the equation:
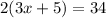
we can apply the distributive property on the left side to get the following:
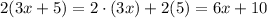
then, we have the following equivalent expression:
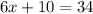
now, to solve for 'x', first we can substract 10 from both sides of the equation to get:
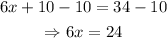
finally, we can divide both sides by 6 to get:
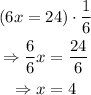
therefore, x = 4