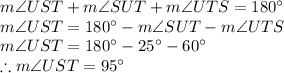Answer:

Explanation:
Givens:
We know that by definition that parallelogram's angles all sum 360°. If we have a diagonal inside, then, we have two triangles, where their angles sum 180°. Also, in this scenario, we have two parallels being crossed by a transversal, which can allow us to deduct several congruences.
So, from the transversal and parallels, we have:
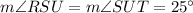 ; because they are alternate interior angles.
; because they are alternate interior angles.
Now, we consider
 , where we already know two angles
, where we already know two angles
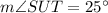 and
and
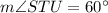 . So, internal angles of a triangle sum 180°, using that we calculate the missing angle ∠UST:
. So, internal angles of a triangle sum 180°, using that we calculate the missing angle ∠UST: