Question

Which of the following describes the graph of y=\sqrt(-4x-36) compared to the parent square root function?

stretched by a factor of 2, reflected over the x-axis, and translated 9 units right
stretched by a factor of 2, reflected over the x-axis, and translated 9 units left
stretched by a factor of 2, reflected over the y-axis, and translated 9 units right
stretched by a factor of 2, reflected over the y-axis, and translated 9 units left

Answer 1

D) stretched by a factor of 2, reflected over the y-axis, and translated 9 units left

Explanation:

its right on edge

Answer 2

Option D - Stretched by a factor of 2, reflected over the y-axis, and translated 9 units left.

Explanation:

Given : The function
`y=√(-4x-36)`

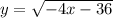
To find : Which of the following describes the graph of
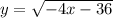`y=√(-4x-36)`compared to the parent square root function?

Solution :

First we simplify the given expression

`y=√(-4x-36)`

`y=√(4(-x-9))`

`y=2√(-(x+9))`

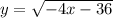
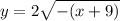
→When we see the original square root function minus was taken outside x and 9 was added from x and 2 was multiplied to the entire function.

• Multiplying 2 in the function will give you the stretched by a factor of 2.

• 
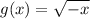  `g(x)=√(-x)` shows the reflection about y-axis i.e, (x,y)→(-x,y).

• If f(x)→f(x+b) then function is shifted left by unit b

⇒ g(x))→g(x+9) then function is shifted left by unit 9

Therefore, The graph of was stretched by a factor of 2, reflected over the y-axis, and translated 9 units left to obtain the graph of the function .

So, Option D is correct.