Question

In the diagram the length of segment TR can be represented by 5x-4.

What is the length os VS?

A) 3 units
B) 11 units
C) 13 units
D) 15 units

Answer 1

Answer: The correct option is D, i.e., 15 units.

Step-by-step explanation:

It is given that the length of segment TR can be represented by 5x-4.

From figure it is noticed that the side TR and RV is equal and the length of segment RV is 2x+5. So,

`5x-4=2x+5`

`3x=9`

`x=3`

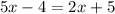
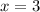
The value of x is 3, so the length of side RV is,

`2x+5=2(3)+5=11`

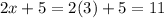
In triangle TRS and angle VRS,

TR=VR

`\angle TRS=\angle VRS=90^(\circ)`

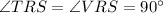
RS=RS (common side)

By SAS rule of congruence triangle,

`\triangle TRS\cong\triangle VRS`

Therefore the side TS and VS are congruent sides.

From figure it is noticed that the length of side TS is 6x-3, therefore the length of side VS is also 6x-3.

`VS=6x-3=6(3)-3=15`

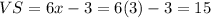
Hence, the length of side VS is 15 units and option D is correct.

Answer 2

Step
`1`

Find the value of x

we know that

TR=RV -------> given problem

in this problem we have

`RV=2x+5\\TR=5x-4`

so

`2x+5=5x-4\\ 5x-2x=5+4\\3x=9\\x=9/3\\x=3\ units`

Step
`2`

In the right triangle TRS

Find the length of the side RS

we know that

Applying the Pythagorean Theorem

`TS^(2) =TR^(2)+RS^(2)\\RS^(2)=TS^(2) -TR^(2)`

in this problem we have

`TS=6x-3\\TR=5x-4`

Substitute the value of x

`TS=6*3-3=15\ units\\TR=5*3-4=11\ units`

`RS^(2)=(15)^(2) -(11)^(2)\\RS^(2)=104\ units^2`

Step
`3`

In the right triangle RSV

Find the length of the side VS

Applying the Pythagorean Theorem

`VS^(2) =RV^(2)+RS^(2)`

in this problem we have

`RV=2x+5=2*3+5=11\ units\\RS^(2)=104\ units^2`

Substitute in the formula

`VS^(2) =11^(2)+104`

`VS^(2)=225\ units^2`

`VS=15\ units`

therefore

the answer is the option D

the value of the side VS is
`15\ units`