Question

6. A police officer with an exceptionally good ear hears an approaching motorcycle. The engine sound he hears as the bike approaches is 195 Hz. (a) Is the actual sound the bike makes higher or lower in pitch? (b) What causes this frequency shift? Indicate with a diagram. (c) Then after the bike passes, he hears 147 Hz as the perceived pitch. If it was a nice sunny 20 °C Day, how fast was the bike moving?

Answer 1

When a wave source is moving with respect to the medium through which the wave propagates, a change in the frequency of the wave in relation to the observer occurs. This effect is known as Doppler Effect.

The relationship between the observed frequency f and emitted frequency f₀ is given by:

`f=(v_s)/(v_s\pm v)f_0`

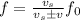
Where v_s is the speed of sound, v is the speed of the source, the minus sign is used when the source is approaching and the plus sign is used when the source is receding.

a)

The observed pitch of an approaching source is higher than the emitted pitch.

Therefore, the actual sound the bike makes is lower in pitch.

b)

The frequency shift is caused by the Doppler Effect.

c)

The speed of sound at 20ºC is 343.3m/s. The observed frequency when the bike approaches is 195Hz and when the bike recedes is 147Hz. Then:

`\begin{gathered} 195Hz=(343.3(m)/(s))/(343.3(m)/(s)-v)f_0 \\ \\ 147Hz=(343.3(m)/(s))/(343.3(m)/(s)+v)f_0 \end{gathered}`

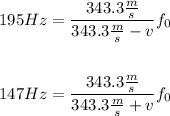
Divide both equations to eliminate f₀, then solve for v:

`\begin{gathered} (195Hz)/(147Hz)=((343.3(m)/(s))/(343.3(m)/(s)-v)f_0)/((343.3(m)/(s))/(343.3(m)/(s)+v)f_0) \\ \\ \Rightarrow(195)/(147)=(343.3(m)/(s)+v)/(343.3(m)/(s)-v) \\ \\ \Rightarrow(195)/(147)(343.3(m)/(s)-v)=343.3(m)/(s)+v \\ \\ \Rightarrow(195)/(147)(343.3(m)/(s))-(195)/(147)v=343.3(m)/(s)+v \\ \\ \Rightarrow(195)/(147)(343.3(m)/(s))-343.3(m)/(s)=(195)/(147)v+v \\ \\ \Rightarrow(343.3(m)/(s))\left((195)/(147)-1\right)=\left((195)/(147)+1\right)v \\ \\ \Rightarrow(343.3(m)/(s))(\left((195)/(147)-1\right))/(\left((195)/(147)+1\right))=v \\ \\ \Rightarrow v=(343.3(m)/(s))(\left((195)/(147)-1\right))/(\left((195)/(147)+1\right)) \\ \\ \Rightarrow v=(343.3(m)/(s))(\left(195-147\right))/(\left(195+147\right)) \\ \\ \Rightarrow v\approx48.2(m)/(s) \end{gathered}`

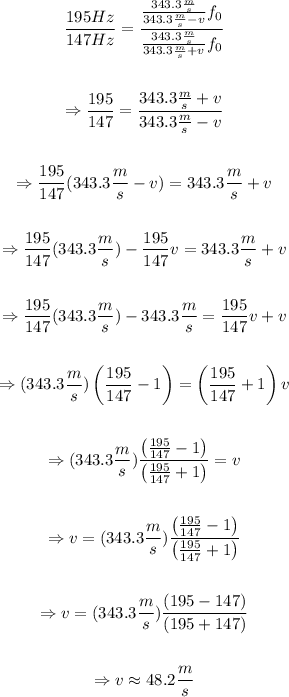
Therefore, the speed of the bike was approximately 48m/s.