Question

R = 8.314 L kPa K-1 mol-1 and 1 atm = 760 mmHg = 101.3 kPa(i) A car tyre has a volume of 10 litres. At 25°C the tyre is inflated to 200 kPa withnitrogen gas. What is the mass of nitrogen gas in the tyre? (ii) What will be the pressure inside the tyre if it is heated to 50°C?

Answer 1

Part i) We will use the ideal gas law to answer this question:

`\begin{gathered} PV=nRT \\ P:pressure\text{ }of\text{ }gas=200\text{ }kPa \\ V:volume=10\text{ }L \\ n:number\text{ }of\text{ }moles \\ R:gasconstant=8.314\text{ }LkPaK^(-1)mol^(-1) \\ T:temperature(273.15K+25\degree C=298.15K) \end{gathered}`

We will determine number of moles of nitrogen gas by using the ideal gas law then use this information to calculate the mass.

`\begin{gathered} n=(PV)/(RT) \\ n=\frac{200kPa*10L}{8.314\text{ }LkPaK^(-1)mol^(-1)*298.15K} \\ n=0.81moles \\ \\ mass=moles* molar\text{ }mass \\ mass=0.81moles*28gmol^(-1) \\ mass=22.68g \end{gathered}`

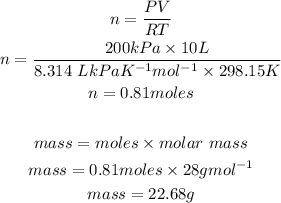
Part i) Answer: The mass of nitrogen gas in the tyre is 22.68g.

Part ii) For this question we will use the ideal gas law as well in addition to the number of moles that was determined in part 1 and the new temperature. The temperature in K is 323.15K

`\begin{gathered} P=(nRT)/(V) \\ P=\frac{0.81mol*8.314\text{ }LkPaK^(-1)mol^(-1)*323.15K}{10L} \\ P=217.62\text{ }kPa \end{gathered}`

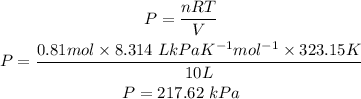
Part ii) Answer: The new pressure will be 217.62 kPa