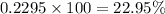Answer: 22.95 %
Explanation:
Given : Scores on a standardized test are normally distributed with
Mean :
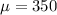
Standard deviation :
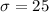
The formula to find z-score:-
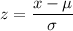
For x=360
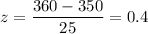
For x=380

The p-value =
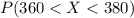

In percent , the percent of students scored between 360 and 380 =