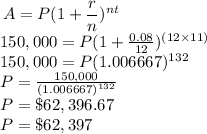Answer:
![\begin{gathered} (A)\Rightarrow P_(pa\imaginaryI d)=\operatorname{\$}127,491.5 \\ (B)\Rightarrow m=\operatorname{\$}22,508.5 \\ (C)\Rightarrow P=\operatorname{\$}62,397 \end{gathered}]()
Step-by-step explanation:
11 years ago a farmer invested his savings for a tractor that resulted in $150,000 in final amount, at the interest rate of 8% annual, compunded monthly. the tractor has a $149,990 sticker price, with a 12% reduction for cash payment.
(A) The farmer pays the following amount:
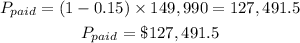
(B) After paying for the tractor, the amount of money left is as follows:
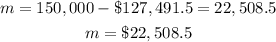
(C) The money that the farmer invested 11 years ago can be determined using the formula (1):
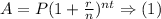
The steps for the solution are as follows: