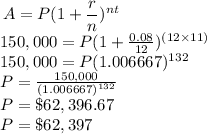Question

A farmer shows up at a tractor dealership with $150,000 to buy a tractor priced at $149,990. The excessafter buying the tractor will be used to pay for license, insurance and maintenance for the first few months.He invested all of his savings 11 years ago to buy this tractor. His investment earned 8% annual interestcompounded monthly. = (1 +R over N)^ntA Since he is paying cash for the tractor he is able to negotiate 12% reduction off the sticker price.How much did he pay for the tractor?B. How much money does he have available for license, insurance and maintenance.C. How much money did he invest 11 years ago to be able to buy the tractor and cover the othercosts? Round your answer to the nearest dollar

Answer 1

Step-by-step explanation:

11 years ago a farmer invested his savings for a tractor that resulted in $150,000 in final amount, at the interest rate of 8% annual, compunded monthly. the tractor has a $149,990 sticker price, with a 12% reduction for cash payment.

(A) The farmer pays the following amount:

`\begin{gathered} P_(paid)=(1-0.15)*149,990=127,491.5 \\ P_(paid)=\$127,491.5 \end{gathered}`

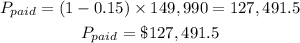
(B) After paying for the tractor, the amount of money left is as follows:

`\begin{gathered} m=150,000-\$127,491.5=22,508.5 \\ m=\$22,508.5 \end{gathered}`

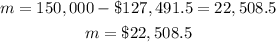
(C) The money that the farmer invested 11 years ago can be determined using the formula (1):

`A=P(1+(r)/(n))^(nt)\Rightarrow(1)`

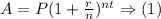
The steps for the solution are as follows:

`\begin{gathered} \begin{equation*} A=P(1+(r)/(n))^(nt) \end{equation*} \\ 150,000=P(1+(0.08)/(12))^((12*11)) \\ 150,000=P(1.006667)^(132) \\ P=(150,000)/((1.006667)^(132)) \\ P=\$62,396.67 \\ P=\$62,397 \end{gathered}`