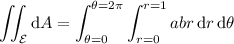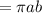The general equation of an ellipse centered at the origin with its semiaxes coinciding with the coordinate axes is given by
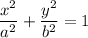
Substituting
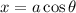
and
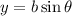
into the above equation gives the Pythagorean identity, so we can use polar coordinates quite nicely to our advantage.
If
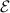
is the ellipse with the equation above, the area is given by the double integral

Let
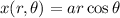
and
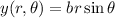
, so that the Jacobian matrix is
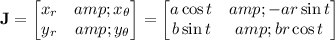
and the magnitude of its determinant is
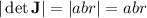
since in polar coordinates we use the convention that

, and
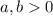
because they are lengths.
Now, the area is given by