Question

Jack is selling tickets to an event. attendees can either buy a general admission ticket or a vip ticket. the general admission tickets are $60 in the vip tickets are $90. he doesn't know how many of each type he has sold, but he knows he sold a total of 29 tickets and made $2100.

Answer 1

x+y=29
60x+90y=2100

substitute the value of x as (29-y) in the second equation
60(29-y) + 90y =2100
30y = 2100-1740=360
y=12 so x=17
so 17 general tickets were sold and 12 vip tickets were sold.

Answer 2

Jack sold 17 admission tickets and 12 vip tickets.

Explanation:

1. Let´s name the variables as:

x=number of admission tickets

y=number of vip tickets

2. As the problem says Jack sold a total of 29 tickets, it can be expressed as:

`x+y=29` (Eq.1)

3. As the general admission tickets are $60, the vip tickets are $90 and he made $2100, it can be expressed as:

`60x+90y=2100` (Eq.2)

4. Solve for x on the Eq.1:

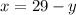`x=29-y` (Eq.3)

5. Replace Eq.3 in Eq.2:

`60(29-y)+90y=2100\\1740-60y+90y=2100\\-60y+90y=2100-1740\\30y=2100-1740\\30y=360\\y=(360)/(30)\\y=12`

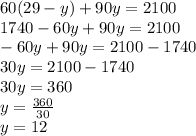
6. Replace the value of y in Eq.3:

`x=29-12\\x=17`

Therefore Jack sold 17 admission tickets and 12 vip tickets.