We are given that a bullet collides with a block and produces a change in height.
Part 1. To determine the change in potential energy we will use the following equation:
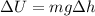
Where:
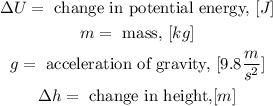
Since the change in height is given as 7.15 cm we will convert this to meters using the following conversion factor:
![100\operatorname{cm}=1m]()
Multiplying by the conversion factor in decimal form we get:
![7.15\operatorname{cm}*\frac{1m}{100\operatorname{cm}}=0.0715m]()
The term "m" for the mass is the sum of the masses of the block and the bullet:
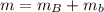
Where:
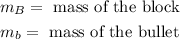
Since the mass of the bullet is given in grams we will covert this to kilograms using the following conversion:
![1000g=1\operatorname{kg}]()
Multiplying by the conversion factor:
![6.25g*\frac{1\operatorname{kg}}{1000\operatorname{kg}}=0.00625\operatorname{kg}]()
Now, we substitute in the formula form the total mass:
![m=1.25\operatorname{kg}+0.00625\operatorname{kg}]()
Solving the operations:
![m=1.25625\operatorname{kg}]()
Substituting in the formula for the change in potential energy:
![\Delta U=(1.25625\operatorname{kg})(9.8(m)/(s^2))(0.0715m)]()
Solving the operations:
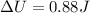
Therefore, the change in potential energy is 0.88 Joules.
Part 2. To determine the velocity immediately after the collision we need to have into account that the kinetic energy of the block/bullet will convert into potential energy, therefore, the kinetic energy is equivalent to the change in potential energy:
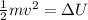
From this, we can solve for "v", first by multiplying both sides by 2:
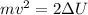
Now, we divide both sides by "m":
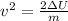
Taking square root to both sides:
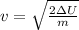
Substituting the values:
![v=\sqrt[]{(2\Delta U)/(m)}](https://img.qammunity.org/qa-images/2023/formulas/physics/college/mfdyj33alu79ksuguj6y.png)
Substituting the values:
![v=\sqrt[]{\frac{2(0.88J)}{1.25625\operatorname{kg}}}]()
Solving the operations:
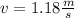
Therefore, the speed of the block/bullet combo is 1.18m/s immediately after the collision.
Part 3. We are asked to determine the speed of the bullet before entering the block. To do that we will use a balance of momentum, as follows:
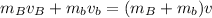
Where:
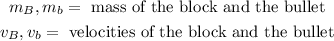
Since the bullet is initially at rest its initial velocity is zero, therefore:
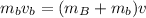
Now, we divide both sides by the mass of the bullet:
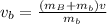
Substituting the values we get:
![v_b=\frac{(1.25625kg)(1.18(m)/(s))}{0.00625\operatorname{kg}}]()
Solving the operations:
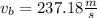
Therefore, the velocity of the bullet is 237.18 meters per second.