Question

A ballistic pendulum consists of a 1.25-kg block of wood that is hanging from the ceiling in such a way that when a bullet enters it, the block’s change in height can be recorded as it swings. A bullet having a mass of 6.25-grams and unknown velocity strikes the block and becomes imbedded in it. The impulse imparted to the block causes it to swing in such a way that its height increases by 7.15 cm.1 What was the change in potential energy of the block/bullet combo after the collision?2What was the speed of the block/bullet combo immediately after the collision (and before it beganto swing)?3What was the speed of the bullet before entering the block of wood?

Answer 1

We are given that a bullet collides with a block and produces a change in height.

Part 1. To determine the change in potential energy we will use the following equation:

`\Delta U=mg\Delta h`

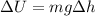
Where:

`\begin{gathered} \Delta U=\text{ change in potential energy, }\lbrack J\rbrack \\ m=\text{ mass, }\lbrack kg\rbrack \\ g=\text{ acceleration of gravity, }\lbrack9.8(m)/(s^2)\rbrack \\ \Delta h=\text{ change in height,}\lbrack m\rbrack \end{gathered}`

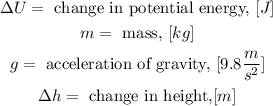
Since the change in height is given as 7.15 cm we will convert this to meters using the following conversion factor:

Multiplying by the conversion factor in decimal form we get:

The term "m" for the mass is the sum of the masses of the block and the bullet:

`m=m_B+m_b`

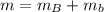
Where:

`\begin{gathered} m_B=\text{ mass of the block} \\ m_b=\text{ mass of the bullet} \end{gathered}`

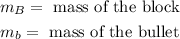
Since the mass of the bullet is given in grams we will covert this to kilograms using the following conversion:

Multiplying by the conversion factor:

Now, we substitute in the formula form the total mass:

Solving the operations:

Substituting in the formula for the change in potential energy:

Solving the operations:

`\Delta U=0.88J`

Therefore, the change in potential energy is 0.88 Joules.

Part 2. To determine the velocity immediately after the collision we need to have into account that the kinetic energy of the block/bullet will convert into potential energy, therefore, the kinetic energy is equivalent to the change in potential energy:

`(1)/(2)mv^2=\Delta U`

From this, we can solve for "v", first by multiplying both sides by 2:

`mv^2=2\Delta U`

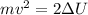
Now, we divide both sides by "m":

`v^2=(2\Delta U)/(m)`

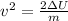
Taking square root to both sides:

`v=\sqrt{(2\Delta U)/(m)}`

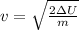
Substituting the values:

`v=\sqrt[]{(2\Delta U)/(m)}`

Substituting the values:

Solving the operations:

`v=1.18(m)/(s)`

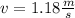
Therefore, the speed of the block/bullet combo is 1.18m/s immediately after the collision.

Part 3. We are asked to determine the speed of the bullet before entering the block. To do that we will use a balance of momentum, as follows:

`m_Bv_B+m_bv_b=(m_B+m_b)v_{}`

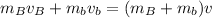
Where:

`\begin{gathered} m_B,m_b=\text{ mass of the block and the bullet} \\ v_B,v_b=\text{ velocities of the block and the bullet} \end{gathered}`

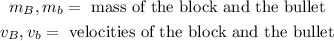
Since the bullet is initially at rest its initial velocity is zero, therefore:

`m_bv_b=(m_B+m_b)v_{}`

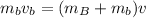
Now, we divide both sides by the mass of the bullet:

`v_b=((m_B+m_b)v)/(m_b)`

Substituting the values we get:

Solving the operations:

`v_b=237.18(m)/(s)`

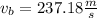
Therefore, the velocity of the bullet is 237.18 meters per second.