Question

The total body surface area, or BSA, of a human is difficult to calculate. There are various models that estimate BSA based on a person's weight and height. One simpler model isBSA =( see picture)where w= weight in kg and h= height in cm. a. Using this model, estimate the height of a person who weighs 76 kg and whose BSA is 1.8. Round your answer to the nearest cm. h=  cm b.  Using this model, estimate the weight of a person who is 164 cm tall and whose BSA is 2.1. Round your answer to the nearest kg. w=  kg

Answer 1

The given equation of BSA is

`\text{BSA}=\sqrt[]{(wh)/(3600)}`

w is the weight in kg

h is the height in cm

a. We need to find the height when

w = 76 kg

BSA = 1.8

Substitute them in the rule above to find h

`1.8=\sqrt[]{(76(h))/(3600)}`

Square both sides to cancel the square root

`\begin{gathered} (1.8)^2=\lbrack\sqrt[]{(76(h))/(3600)}\rbrack^2 \\ 3.24=(76h)/(3600) \end{gathered}`

Multiply both sides by 3600

`\begin{gathered} 3.24(3600)=(76h)/(3600)(3600) \\ 11664=76h \end{gathered}`

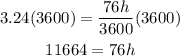
Divide both sides by 76 to find h

`\begin{gathered} (11664)/(76)=(76h)/(76) \\ 153.4736842=h \end{gathered}`

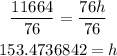
Round it to the nearest cm

h = 153 cm

b. We need to find the weight when

h = 164 cm

BSA = 2.1

Substitute them in the equation

`2.1=\sqrt[]{(164w)/(3600)}`

We will do the same steps above

`\begin{gathered} (2.1)^2=\lbrack\sqrt[]{(164w)/(3600)}\rbrack^2 \\ 4.41=(164w)/(3600) \end{gathered}`
`\begin{gathered} 4.41(3600)=(164w)/(3600)(3600) \\ 15876=164w \end{gathered}`
`\begin{gathered} (15876)/(164)=(164w)/(164) \\ 96.80487805=w \end{gathered}`

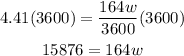
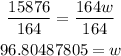
Round it to the nearest kg

w = 97 kg