Let the measure of side AB be x, then, the measue of side AE is given by
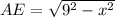
.
Now, ABCD is a square of size x, thus the area of square ABCD is given by

Also, AEFG is a square of size
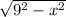
, thus, the area of square AEFG is given by
 The sum of the areas of the two squares ABCD and AEFG is given by
The sum of the areas of the two squares ABCD and AEFG is given by

Therefore, the number of square units in the sum of the areas of the two squares ABCD and AEFG is 81 square units.