Question

A television sports commentator wants to estimate the proportion of citizens who​ "follow professional​ football." complete parts​ (a) through​ (c).

Answer 1

Part A

The number of samples needed to get a confidence interval with a margin of error M is given by:


`n= (z_(\alpha/2)^2p(1-p))/(M^2)`

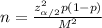
where
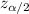
`z_(\alpha/2)` is the z-score of the confidence level and p is the population proportion.

If he wants to be within 4 percentage points with 96% confidence and he uses an estimate of 48% obtained from a poll, the sample size that should be obtained is given by:


`n= ((2.054)^2*0.48(1-0.48))/((0.04)^2) \\ \\ = (4.218916*0.48(0.52))/(0.0016) = (1.053041434)/(0.0016) \\ \\ =\lceil658.15\rceil=659`



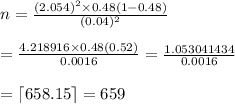
Part B:

If he wants to be within 4 percentage points with 96% confidence and he does not use any prior estimates, the sample size that should be obtained is given by:


`n= ((2.054)^2*0.50(1-0.50))/((0.04)^2) \\ \\ = (4.218916*0.50(0.50))/(0.0016) = (1.054729)/(0.0016) \\ \\ =\lceil659.21\rceil=660`



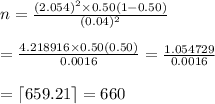
Part C:

The resulta from parts a and b are close because the result from the poll (i.e. 48%) is close to the conservative proportion used when there is no prior knowledge of any proportion (i.e. 50%).