Question

If the polynomials ax^3 + 4x^2 + 3x - 5 and x^3 - 3x^2 - 5x + a leave the same remainder when divided by (x-3) and (x+2) respectively, find the value of a.....

Answer 1

Given:

The polynomials
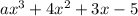`ax^3+4x^2+3x-5` and
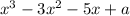`x^3-3x^2-5x+a` leave the same remainder when divided by (x-3) and (x+2) respectively.

To find:

The value of a.

Solution:

Remainder theorem: If a polynomial p(x) is divided by (x-c), then the remainder is equal to p(c).

The polynomials
`f(x)=ax^3+4x^2+3x-5` is divided by (x-3). So, the remainder is f(3).

`f(3)=a(3)^3+4(3)^2+3(3)-5`

`f(3)=27a+36+9-5`

`f(3)=27a+40`

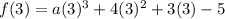
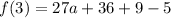
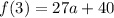
The polynomial
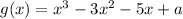`g(x)=x^3-3x^2-5x+a` is divided by (x+2). So, the remainder is g(-2).

`g(-2)=(-2)^3-3(-2)^2-5(-2)+a`

`g(-2)=-8-12+10+a`

`g(-2)=-10+a`

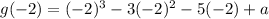
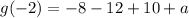
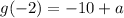
It is given that the remainders are same. So,

`f(3)=g(-2)`

`27a+40=-10+a`

`27a-a=-10-40`

`26a=-50`

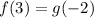
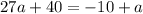
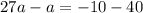
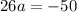
Divide both sides by 26.

`a=(-50)/(26)`

`a=(-25)/(13)`

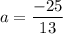
Therefore, the value of a is
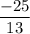`(-25)/(13)`.