1 Answer

← Prev Question Next Question →

Ask a Question

Nitin Patel · Answer 1 · 2018-09-01T01:31:20+0000

first off, what's the slope of "r" anyway,
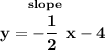
$\bf y=\stackrel{slope}{-\cfrac{1}{2}}x-4$ .

low and behold, since "r" is in slope-intercept form, notice, it has a slope of -1/2.

now, any line perpendicular to "r", will have a negative reciprocal slope to it, that is,

$\bf \textit{perpendicular, negative-reciprocal slope for slope}\quad -\cfrac{1}{2}\\\\ negative\implies +\cfrac{1}{{{ 2}}}\qquad reciprocal\implies + \cfrac{{{ 2}}}{1}\implies 2$

so we're really looking for a line whose slope is 2, and runs through 4,-3,

$\bf \begin{array}{ccccccccc} &&x_1&&y_1\\ % (a,b) &&(~{{ 4}} &,&{{ -3}}~) \end{array} \\\\\\ % slope = m slope = {{ m}}\implies 2 \\\\\\ % point-slope intercept \stackrel{\textit{point-slope form}}{y-{{ y_1}}={{ m}}(x-{{ x_1}})}\implies y-(-3)=2(x-4)\implies y+3=2x-8 \\\\\\ y=2x-11$

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

No related questions found

Other Questions