Greetings!Convert the equation to
slope y-intercept form:
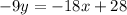
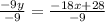
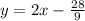
The Slope of this equation is represented by
2 (or
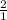
). In order to create a line perpendicular to this line, they must have
negative reciprocals. The formula for this is:
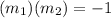
(m represents the slope each line).
Input the values we know:
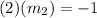 Solve
Solve:
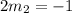
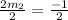
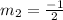 Arrange
Arrange the new equation in
slope y-intercept form:
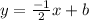 Input
Input a coordinate point into the equation:
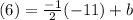 Solve
Solve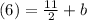

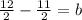

The
y-intercept is equal to
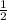
Now using the information we have, arrange the equation in
slope y-intercept form:
![\left[\begin{array}{ccc}y= (-1)/(2)x+ (1)/(2) \end{array}\right]](https://img.qammunity.org/2018/formulas/mathematics/high-school/3f1x7no7eti2q263els8vws0ugj6k19ad0.png)
Hope this helps!
-Benjamin