Question

A phonograph record 30.0cm in diameter rotates 33.5 times per minute.

What is its frequency?

What is its period?

What is the linear speed of a point on its rim?

What is the centripetal acceleration of a point on its rim?

Answer 1

The frequency (f) is 33.5 rpm, as given, or 0.59 rev/sec. The period of rotation (T) is 1/f, so 1/0.59 or ~ 1.69 seconds. The linear speed (v) of a point on it's rim is calculated using v= 2*pi*r/T so, v= 2 * pi * (30/2) / 1.69 ==> 2 * 3.14 * 15 / 1.69 ==> 55.74 cm/s. The centripetal acceleration (a) of a point on it's rim is caluclated using a = v^2/r so a = 55.74 ^2 / 15 ==> 207.13 cm/s^2

Answer 2

Step-by-step explanation:

Given that phonograph rotates 33.5 times per minute:

Frequency of the phonograph =
`33.5 min^(-1)`

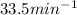
Time period =
`(1)/(frequency)=(1)/(33.5 min^(-1))=0.0298 min`

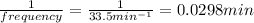
time period = 0.0298 × 60 seconds =1.788 seconds

Radius r = 15 cm = 0.15 m (1 m = 100 cm)

The linear speed =
`(Distance)/(time)=(2\pi* r)/(1.788 sec)=(2* 3.14* 0.15 m)/(1.788 sec)=0.526 m/s`

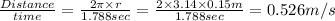
The centripetal acceleration of a point on its rim:

`\frac{(\text{linear velocity})^2}{\text{radius of the rim}}=((0.526 m/s)^2)/(0.15 m)=1.84 m/s^2`

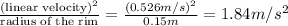
Centripetal acceleration is
`1.84 m/s^2`.