Question

At the end of an advertising campaign, weekly sales declined according to the equation y=19,000(5−0.04x) dollars, where x is the number of weeks after the end of the campaign.a. Determine the sales at the end of the ad campaign.b. Determine the sales 7 weeks after the end of the campaign.c. Does this model indicate that sales will eventually reach $0?

Answer 1

The function that gives us the weekly sales in dollars as a function of the number of weeks after the end of the ad campaign is

`y=19000(5^(-0.04x))`

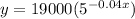
a)

Just after the end of the ad campaign, x=0 (Immediately after the campaign, not even a day has passed). Then, set x=0 and solve for y as shown below

`\begin{gathered} x=0 \\ \Rightarrow y=19000(5^(-0.04(0)))=19000(5^0)=19000(1)=19000 \\ \Rightarrow y(0)=19000 \end{gathered}`

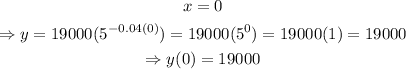
The answer to part a is 19000

b) 7 weeks after the end of the campaign is equivalent to set x=7 and solving for y

`\begin{gathered} x=7 \\ \Rightarrow y(7)=19000(5^(-0.04(7)))=19000(5^(-0.28))=12107.15213\ldots\approx12107.15 \\ \Rightarrow y(7)=12107.15 \end{gathered}`

The answer to part b is 12107.15.

c) Set y=0 and solve for x, as shown below

`\begin{gathered} 0=19000(5^(-0.04x)) \\ \Rightarrow5^(-0.04x)=0 \\ \Rightarrow x\to\infty \end{gathered}`

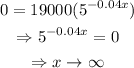
The sales reach a value of zero after an infinite number of weeks.

Sales can never reach zero because an infinite number of weeks would be needed for that to happen.