The function that gives us the weekly sales in dollars as a function of the number of weeks after the end of the ad campaign is
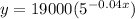
a)
Just after the end of the ad campaign, x=0 (Immediately after the campaign, not even a day has passed). Then, set x=0 and solve for y as shown below
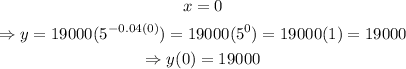
The answer to part a is 19000
b) 7 weeks after the end of the campaign is equivalent to set x=7 and solving for y
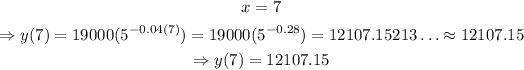
The answer to part b is 12107.15.
c) Set y=0 and solve for x, as shown below
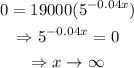
The sales reach a value of zero after an infinite number of weeks.
Sales can never reach zero because an infinite number of weeks would be needed for that to happen.