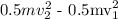So here, we use the equation:
W = ΔKE + ΔPE
Recall that: KE = 0.5mv^2, and PE = qdΔV/D
ΔKE = 0.5m(v2)^2 - 0.5m(v1)^2, where v2 and v1 are Initial and final velocity respectively.
ΔPE = PE2 - PE1
PE2 = 0, since all energy is converted to other forms, mainly kinetic energy.
PE1 = q(d1)ΔV/D
Here, W = 0.
0 = 0.5m(v2)^2 - 0.5m(v1)^2 + 0 - q(d1)ΔV/D
Simplifying a bit, and knowing that d1 = D,
0 = 0.5m((v2)^2 - (v1)^2) - qΔV
Moving qΔV to the other side,
qΔV = 0.5m((v2)^2 - (v1)^2)
Dividing by q and isolating ΔV,
ΔV = 0.5m * ((v2)^2 - (v1)^2) / q
Now, we have ΔV, which is the electric potential difference, in terms of all the variables we know.
m = 9.1 * 10^-31
v2 = 1 * 10^6
v1 = 5 * 10^6
q = 1.602 * 10^-19 (this is a well known constant)
ΔV = 0.5*9.1*10^-31 * ((5*10^6)^2 - (1*10^6)^2) / 1.602*10^-19
Solving and simplifying all of this, we get that
ΔV = 68.25 V