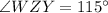Answer:
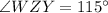
Explanation: Since, here WXYZ is a kite where
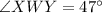 and
and
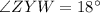
Thus according to the property of a kite ,
Exactly one pair of opposite angles are equal and The main diagonal bisects a pair of opposite angles.
Therefore, In kite WXYZ ,
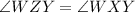 -------(1)
-------(1)
And, WY is the angle bisector of kite WXYZ.
So,
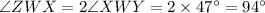 ( because WY bisects
( because WY bisects
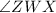 into two equal angles
into two equal angles
 and
and
 )
)
⇒
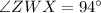 -----(2)
-----(2)
Similarly,
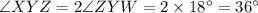
⇒
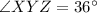 -----(3)
-----(3)
Since, WXYZ is a kite ⇒
 -------(4)
-------(4)
Therefore, From equation (1), (2), (3) and (4),
We get,