Question

​ AD​ , BD , and CD are angle bisectors of the sides of △ABC . BE=12 m and BD=20 m.

What is DG ?

Answer 1

The answer is 16

And also , can people please stop posting did you get the answer yet, just so you could get the points. They only take two answers, and that's a waste of somebody who could've answered or helped.

Answer 2

DG=16 m

Explanation:

Given: AD, BD and Cd are the angle bisectors of the sides of ΔABC and B=12m and BD=20m.

To find: The value of DG.

Solution: It is given that AD, BD and Cd are the angle bisectors of the sides of ΔABC and B=12m and BD=20m, then from the ΔBED, we have

`(BD)^(2)=(BE)^(2)+(ED)^(2)`

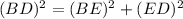
Substituting the given values, we have

`(20)^2=(12)^2+(ED)^2`

`400=144=(ED)^2`

`400-144=(ED)^2`

`256=(ED)^2`

`16 m=ED`

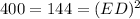
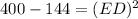
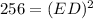
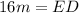
Thus, the value of ED is 16m.

Now, we know that the distance from the mid points of the sides of the given triangle to the circumcenter D are equal, thus

ED=DG

ED=DG=16

Therefore, the value of DG is 16m.