Question

Assume there are 365 days in a year.

What is the probability that ten students in a class have different birthdays?
What is the probability that among ten students in a class, at least two of them share a birthday?

Answer 1

1) The probability that ten students in a class have different birthdays is 0.883.

2) The probability that among ten students in a class, at least two of them share a birthday is 0.002.

Explanation:

Given : Assume there are 365 days in a year.

To find : 1) What is the probability that ten students in a class have different birthdays?

2) What is the probability that among ten students in a class, at least two of them share a birthday?

Solution :

`\text{Probability}=\frac{\text{Favorable outcome}}{\text{Total number of outcome}}`

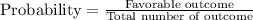
Total outcome = 365

1) Probability that ten students in a class have different birthdays is

The first student can have the birthday on any of the 365 days, the second one only 364/365 and so on...

`(364)/(365)* (363)/(365) * (362)/(365) * (361)/(365)*(360)/(365) * (359)/(365) * (358)/(365) * (357)/(365) *(356)/(365)=0.883`

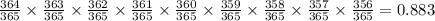
The probability that ten students in a class have different birthdays is 0.883.

2) The probability that among ten students in a class, at least two of them share a birthday

P(2 born on same day) = 1- P( 2 not born on same day)

`\text{P(2 born on same day) }=1-[(365)/(365)* (364)/(365)]`

`\text{P(2 born on same day) }=1-[(364)/(365)]`

`\text{P(2 born on same day) }=0.002`

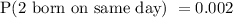
The probability that among ten students in a class, at least two of them share a birthday is 0.002.