Question

What is the area of trapezoid ABCD ?

Enter your answer as a decimal or whole number in the box. Do not round at any steps.

Answer 1

AD = 5
BC = 15
AB = 5

Area = 1/2(AD + BC)*AB
Area = 1/2(5 + 15)(5)
Area = 1/2(20)(5)
Area = 50

Answer 2

Area of the trap-ezoid is
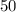`50` square units

Step-by-step explanation

The given trap-ezoid has vertices
`A(-2,2)`,
`B(2,5)`,
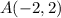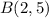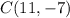`C(11,-7)` and
`D(1,-2)`.

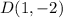Area of a trap-ezoid is given by

`Area =(1)/(2)(sum\:of\: paralle\:sides)* \:vertical\: height`

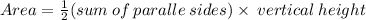
We use the distance formula to determine length of all the necessary sides and plug them in to the formula.

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

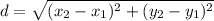
The vertical height of the trap-ezoid is

`|AB|=√((2--2)^2+(5-2)^2)`

`|AB|=√((2+2)^2+(5-2)^2)`

`|AB|=√((4)^2+(3)^2)`

`|AB|=√(16+9)`

`|AB|=√(25)`

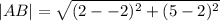
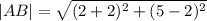
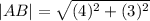
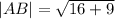
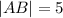`|AB|=5` units

The length of the parallel sides are;

`|AD|=√((1--2)^2+(-2-2)^2)`

`|AD|=√((3)^2+(-4)^2)`

`|AD|=√(9+16)`

`|AD|=√(25)`

`|AD|=5`

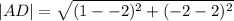
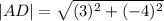
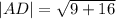
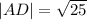
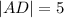
and

`|BC|=√((11-2)^2+(-7-5)^2)`

`|BC|=√((9)^2+(-12)^2)`

`|BC|=√(81+144)`

`|BC|=√(225)`

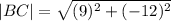
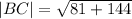
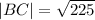
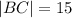`|BC|=15` units

we now substitute all these values to obtain,

`Area =(1)/(2)(15+5)* 5`

`Area =(1)/(2)(20)* 5`

`Area =(10)* 5`

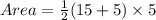
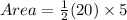
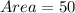`Area =50` square units.