Question

Which additional fact proves that ΔRST and ΔWXY are congruent if ∠R ≅ ∠W and RS ≅ WX.

∠R = 2x + 3
∠S = x + 10
∠T = 3x - 13
A) ∠X = x + 33
B) ∠Y = x + 33
C) ∠X = 2x - 20
D) ∠Y = 2x - 20

Answer 1

Answer:c

Explanation:

Answer 2

C)
`\angle X=2x-20`

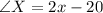
Explanation:

We are given that

`\angle R\cong \angle W`

`RS\cong WX`

`\angle R=2x+3`

`\angle S=x+10`

`\angle T=3x-13`

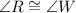
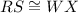
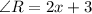
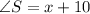
We have to find the additional fact which proves that triangle RST and triangle WXY are congruent.

In triangle RST

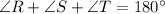`\angle R+\angle S+\angle T=180^(\circ)` (Triangle angles sum property)

Substitute the values then we get

`2x+3+x+10+3x-13=180`

`6x=180`

`x=(180)/(6)=30^(\circ)`

`\angle R=2(30)+3=63^(\circ)`

`\angle S=30+10=40^(\circ)`

`\angle T=3(30)-13=73^(\circ)`

`\angle R=\angle W=63^(\circ)`

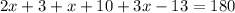
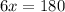
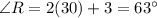
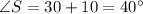
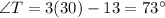
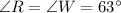
When two triangles are congruent then each part of one triangle is congruent to its corresponding parts of another triangle.

Therefore, if
`\triangle RST\cong \triangle WXY`

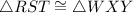
Then,
`\angle S\cong \angle X, \angle T\cong \angle Y`

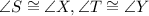
Therefore,
`\angle Y=73^(\circ)`

`\angle X=40^(\circ)`

`\angle X=2(30)-20=40^(\circ)`

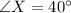
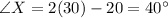
Hence, option C is correct.