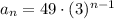Question

A recursive rule for a geometric sequence is a1=4/9;an=3an−1

What is the explicit rule for this sequence?



Enter your answer in the box.

Answer 1

the answer is (4/9)(3)^n-1

Answer 2

Explicit rule for this sequence is,
`a_n = 49\cdot (3)^(n-1)`

Explanation:

A recursive rule for a geometric sequence is
`a_1=49`,
`a_n = 3a_(n-1)`

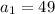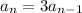
First term
`a_1= 49`

To get second term, just multiply the first term by 3

`a_n = 3 a_(n-1)`

`a_2 = 3 a_1`

`a_2= 3\cdot 49`

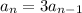
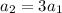
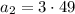
so, we get the common ratio r = 3

Now, Explicit rule for geometric sequence is given by:

`a_n = a_1 \cdot (r)^(n-1)`

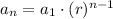
Here,
`a_1= 49` and r= 3

So, explicit rule is :

`a_n = 49\cdot (3)^(n-1)`