Question

How can you tell whether a rational function has a slant asymptote without doing any division?Be sure to show and explain all work.

Answer 1

Check if the degree of the polynomial on the numerator is one unit greater than the degree of the polynomial on the denominator.

1) In this problem, we need to understand that the slant asymptote is defined by the degree of the polynomial on the numerator. So, considering that the degree of the polynomial in the numerator is one unit more than the degree of the polynomial in the denominator.

For example:

`y=(x^2-4)/(x+3)`

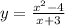
Since the degree of the numerator is 2, and the degree of the polynomial in the denominator is 1, then we can state that there is a slant asymptote in this rational function.

2) Thus, the answer is:

We can tell by checking if the degree of the polynomial on the numerator is one unit greater than the degree on the denominator.