Question

Path of a ball after kicked from a height of .5 m above ground is given by h=-0.1d^2+1.1d+.5 (h-height above ground, d-horizontal distance)?

How far has the ball travelled horizontally, to the nearest tenth metre, when it lands?

Answer 1

The function is the following:


`h(d)=-0.1d^2+1.1d+0.5`.

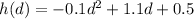
This is a function of the height of the ball, in terms of d, the horizontal distance.


When the ball lands, h is equal to 0, so we need to find the value of d for which h(d) is 0, so we need to solve the equation:


`-0.1d^2+1.1d+0.5=0`.

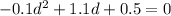
Thus, we have a quadratic equation to solve: we use the discriminant formula!

a=-0.1, b=1.1, c=0.5, thus the discriminant is
`D=b^2-4ac=(1.1)^2-4(-0.1)(0.5)=1.21+0.2=1.41`.

The square root of 1.41 is approximately 1.19,

thus, the roots of the equation are:


`d_1= (-1.1+1.19)/(2(-0.1))= (0.09)/(-0.2)= -0.45`



`d_2= (-1.1-1.19)/(2(-0.1))= (-2.29)/(-0.2)= 11.45`


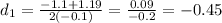
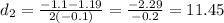
stance must be positive, so we only consider the second answer. Thus, d=11.5 m


Answer: 11.5

Answer 2

We are given the equation that describes the height as follows:
h = -0.1 d^2 + 1.1d + 0.5

When the ball lands, its height becomes zero, therefore:
To get the distance, we will simply substitute with h=0 in the equation and then factorize it to get the possible distance values as follows:
0 = -0.1 d^2 + 1.1d + 0.5
(x-11.44)(x+0.44) = 0
either the distance x = 11.44 m (accepted value)
or x = -0.44 m (rejected value as distance cannot be 0)