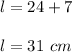Question

The length of a rectangle is 7 more than the width the area is 744 square centimeters find length and width of rectangle

Answer 1

`l=31\ cm\\\\w=24\ cm`

Explanation:

The formula that is used to calculate the area of a rectangle is:

`A=lw`

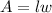
Where "l" is the lenght and "w" is the width.

You know that the area of that rectangle is:

`A=744\ cm^2`

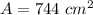
And, according to the exercise, its lenght is 7 more than its width; then:

`l=w+7`

Then, you can make the corresponding substitution into the formula
`A=lw`:

`744=(w+7)w`

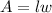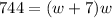
Simplify:

`744=w^2+7w\\\\w^2+7w-744=0`

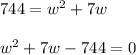
Factor the equation. Find two numbers whose sum is 7 and whose product is -744. These are 31 and -24.

Then, you get:

`(w-24)(w+31)=0\\\\w_1=24\\\\w_2=-31`

The width of the rectangle is the positive value:

`w=24\ cm`

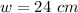
Then, the lenght is:

`l=24+7\\\\l=31\ cm`