Question

A person rides a Ferris wheel that turns with constant angular velocity. Her weight is 481.0 N. At the top of the ride her apparent weight is 1.500 N different from her true weight.A. What is her apparent weight at the top of the ride?B. What is her apparent weight at the bottom of the ride?C. If the angular speed of the Ferris wheel is 0.0250 rad/s, what is its radius?

Answer 1

Given data

*The given true weight is W = 481.0 N

*Difference in weight at the top of the ride is N = 1.50 N

*The angular speed of the Ferris wheel is

`\omega=0.0250\text{ rad/s}`

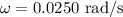
(A)

The apparent weight at the top of the ride is calculated as

`\begin{gathered} W_t=W-N \\ =481.0-1.50 \\ =479.5\text{ N} \end{gathered}`

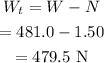
Hence, the apparent weight at the top of the ride is W_t = 479.5 N

(B)

The apparent weight at the bottom of the ride is calculated as

`\begin{gathered} W_b=W+N \\ =481.0+1.50 \\ =482.5\text{ N} \end{gathered}`

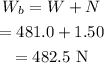
Hence, the apparent weight at the bottom of the ride is W_b = 482.5 N

(C)

The mass of the person is calculated as

`\begin{gathered} m=(W)/(g) \\ =(481.0)/(9.8) \\ =49.08\text{ kg} \end{gathered}`

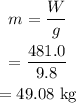
The radius of the Ferris wheel is calculated as

`\begin{gathered} N=mr\omega^2 \\ r=(N)/(m\omega^2) \end{gathered}`

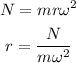
Substitute the known values in the above expression as

`\begin{gathered} r=(1.5)/(49.08*(0.0250)^2) \\ =48.89\text{ m} \end{gathered}`

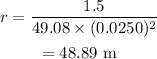
Hence, the radius of the Ferris wheel is r = 48.89 m