Question

This is exponential growth and decay

Answer 1

Given:

In 1999, the number of mosquitos = 2500

They tripled every year.

To find:

The model for this situation and find the number of mosquitos in 2005.

Solution:

The general exponential modal is

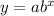`y=ab^x` ...(i)

Where, a is the initial value and 0<b<1 is decay factor and b>1 is growth factor.

In 1999, the number of mosquitos is 2500.

Initial value:
`a=2500`

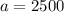
They tripled every year. So, growth factor is 3>1 and it is exponential growth.

Growth factor:
`b=3`

Putting
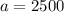`a=2500` and
`b=3` in (i), we get

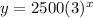`y=2500(3)^x` ...(ii)

Here, y is the population of mosquitos after x year of 1999.

Therefore, the required exponential growth modal is
`y=2500(3)^x`.

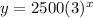We know that,

`2005-1999=6`

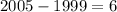
Putting x=6 in (ii), we get

`y=2500(3)^6`

`y=2500(729)`

`y=1822500`

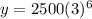
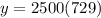
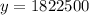
Therefore, the estimated number of mosquitos in 2005 is 1822500.