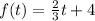Question

The table represents the function f(x).

Which function of t has the same slope and y-intercept as
f(t) = t + 4
f(t) = t – 6
f(t) = 2t + 4
f(t) = 2t + 6

Answer 1

f(t) = 2/3 t + 4

Answer 2

Step 1

Find the slope of the function f(x)

we know that

The formula to calculate the slope between two points is equal to

`m=(y2-y1)/(x2-x1)`

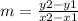
Let

`A(-6,0)\\B(0,4)`

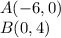
substitute

`m=(4-0)/(0+6)`

`m=(4)/(6)`

`m=(2)/(3)`

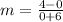
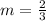
Step 2

Find the y-intercept of the function f(x)

The y-intercept is the value of the function when the value of x is equal to zero

in this problem the y-intercept of the function is the point
`B(0,4)`

so

the y-intercept is equal to
`4`

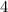
Step 3

Verify each case

we know that

the equation of the line into slope-intercept form is equal to

`y=mx+b`

where

m is the slope

b is the y-intercept

case A)
`f(t)=t+4`

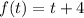
In this case we have

`m=1\\y-intercept=4`

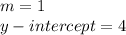
therefore

the function of case A) does not have the same slope as the function f(x)

case B)
`f(t)=t-6`

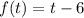
In this case we have

`m=1\\y-intercept=-6`

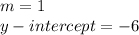
therefore

the function of case B) does not have the same slope and y-intercept as the function f(x)

case C)
`f(t)=(2)/(3)t+4`

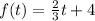
In this case we have

`m=(2)/(3)\\y-intercept=4`

therefore

the function of case C) does have the same slope and y-intercept as the function f(x)

case D)
`f(t)=(2)/(3)t+6`

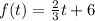
In this case we have

`m=(2)/(3)\\y-intercept=6`

therefore

the function of case D) does not have the same y-intercept as the function f(x)

therefore

the answer is

`f(t)=(2)/(3)t+4`