Question

Assume that different groups of couples use a particular method of gender selection and each couple gives birth to one baby. This method is designed to increase the likelihood that each baby will be a girl, but assume that the method has no effect, so the probability of a girl is 0.5. Assume that the groups consist of 23 couples. Find the mean and the standard deviation for the numbers of girls in groups of 23 Assume that different groups of couples use a particular method of gender selection and each couple gives birth to one baby. This method is designed to increase the likelihood that each baby will be a girl, but assume that the method has no effect, so the probability of a girl is 0.5. Assume that the groups consist of 23 couples. b. Use the range rule of thumb to find the values separating results that are significantly low or significantly high.

Answer 1

The probability excercise assumes experiments that are independent without repetition. In this case each experiment to get a baby will have a success if it were a girl with probability 0.5, then you have a binomial distribution with n=23 and p=0.5. Then

`\begin{gathered} \bar{x}=Np=23(0.5)=11.5\text{ and} \\ \sigma=√(Np(1-p))=√(11.5(0.5))=\sqrt{(23)/(2)((1)/(2))}=\sqrt{(23)/(4)}=(√(23))/(2) \end{gathered}`

The range rule of thumb defines the range about four times the standard deviation, that in this case the range is the difference between the significantly high and low results. It means that

`max{}\lbrace data\rbrace-min\lbrace data\rbrace\approx4\sigma=(4√(23))/(2)=2√(23)\approx9.6`

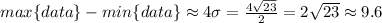
Then also for the range rule you have that the values around the mean are given by

`\begin{gathered} \bar{x}-2\sigma=(23)/(2)-(2√(23))/(2)=(23-2√(23))/(2)\approx6.70\text{ and} \\ \bar{x}+2\sigma=(23)/(2)+(2√(23))/(2)=(23+2√(23))/(2)\approx16.30 \end{gathered}`

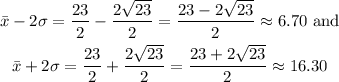
The range rule is really usefull because it indicates that most values would be in the area that is covered by four standard deviation, in other words two times the standard deviation after the mean and two times the standar deviation before the mean you will get the results that are significantly high and significantly low respectively.

Then values of 6.7 girls or FEWER are significantly low and the values of 16.30 girls or GREATER are significantly high.