Answer:
Option C
Explanation:
We are given that an equation
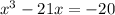
We have to find the root of given polynomial equation by using rational root theorem.
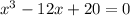
Factor of 1 is 1.
Factors of 20 are
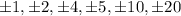
The roots of given polynomial is in the form
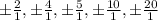
When we substitute x=1 then we get
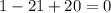
Therefore, 1 is a root of given polynomial.
Hence, option C is correct.